„Nekoliko lopova je ukralo više rolni svile i pri podeli plena su uvideli da ako svaki uzme po 6 rolni da će im ostati 5, a ako svaki uzme po 7 da im nedostaje 8 rolni. Koliko je bilo lopova i koliko rolni svile su uzeli?“ Ovako je glasio jedan od zadataka koji su još od 6. veka nove ere postavljani kineskim činovnicima kao deo ispita za napredovanje u službi, navodi se u studiji dr Vesne Jevremović iz Matematičkog instituta SANU o specifičnom razvoju kineske matematike, čije su osobenosti vidljive i danas.
Najstariji tragovi upotrebe matematike u Kini pronađeni su na životinjskim kostima, najčešće kornjačinim oklopima, upotrebljavanim za proročanstva. Ovi zapisi, koji uključuju i matematičke proračune, nastali su za vreme Šang dinastije, od 16. do 11. veka pre nove ere. Drevni Kinezi su utemeljili matematiku na drugačijim osnovama od antičkih Grka. Kod njih nema aksioma i dedukcija, a izvođenje dokaza, koje je veoma različito od zapadnog načina razmišljanja, izaziva čuđenje, ali pre svega divljenje kakve su sve matematičke probleme umeli da reše, ističe se u studiji dr Vesne Jevremović iz Matematičkog instituta SANU o specifičnom razvoju kineske matematike.
Matematiku najmnogoljudnije nacije od najranijih vremena odlikuje težnja za rešavanjem konkretnih životnih problema. Antički Kinezi se ne bave akademskim raspravama već zemljišnim merama, kalendarom, porezima, arhitekturom i drugim problemima od neposredne praktične koristi. Pored toga, kineski zadaci su izuzetno slikoviti, „a mnogi imaju i posebna imena, tako da se tačno znalo koji se zadatak podrazumeva pod nekim naslovom“. Ipak, možda je najveća neobičnost zapadnjačkom umu to da su stari kineski zadaci u potpunosti tekstualni, a to je slučaj i sa rešenjima, pa danas njihovo rešavanje zahteva da se prvo prevedu na jezik formula.
U nauci su i dalje suprotstavljena mišljenja u kojoj meri je razvoj antičke Kine bio izolovan, odnosno da li se već tada odvijala razmena ideja sa drugim drevnim civilizacijama poput Indije, Egipta, Mesopotamije i Grčke. Na veze među starim narodima ukazuje i trgovački Put svile, koji je ,,otvoren“ 121. godine pre nove ere i koji je spajao Kinu i zemlje na Zapadu, sve do Mediterana. Dokazano je da su neka otkrića u matematici u drugim kulturama potekla iz Kine, ali su mnoga specifična samo za kinesku tradiciju.
Debljina svilene niti
Problem sa arheološkim dokazima o praistoriji kineske matematike je u tome što su Kinezi svoje računice zapisivali na bambusovim pločicama, koje se teško održavaju tokom dužeg vremenskog perioda za razliku od, na primer, glinenih pločica iz Mesopotamije. Dodatno, prvi kineski car Čin Ši Huangdi, koji je pod svojom vlašću ujedinio celu današnju Kinu, u borbi protiv konfučijanskog uticaja je naredio 213. godine pre nove ere da se pobiju naučnici i spale mnogobrojni spisi, među kojima su bili i oni iz matematike. Jedna od retkih matematičkih knjiga koja je opstala iz tog perioda je ”Suan šu šu” („Knjiga o računanju“). Knjiga, pisana na bambusovim pločicama, potiče iz perioda od oko 200 godina pre nove ere, a pronađena je 1983. u jednoj grobnici za koju je pouzdano utvrđeno da je zapečaćena 186. godine pre nove ere.
Do 4. veka pre nove ere već su u upotrebi jedinstvene kineske računaljke, a Kinezi su vrlo rano ovladali jednačinama, negativnim brojevima i algebrom uopšte. Najstarije poznato geomatrijsko delo „Mo đing“ napisao je Mo Cu (470. do 391. godine pre nove ere), a neki matematičari veruju da su ovom delu morala prethoditi druga geometrijska dela koja nisu sačuvana. U knjizi je data definicija geometrijske tačke kao najmanje jedinice koja se ne može deliti i definicije za obim, prečnik i zapreminu.
U kasnijem periodu je sačuvan daleko veći broj matematičkih spisa, koji, između ostalog, potvrđuju da je matematika bila veoma cenjena u Kini i da su tu vrstu obrazovanja, slično filozofiji, dobijali samo odabrani učenici. U jednoj od pronađenih knjiga o astronomiji sa početka nove ere se eksplicitno navodi da je „sposobnost zaključivanja i uopštavanja obeležje inteligentne osobe“. Već od 6. veka, matematika je bila deo ispita koji se polagao radi prijema u državnu službu i kasnijeg napredovanja u državnoj hijerarhiji.
Stari Kinezi su razvili merne jedinice za dužinu, površinu, zapreminu i težinu u velikom rasponu. Imali su posebne nazive za veoma velike brojeve i tačno su znali šta ti brojevi predstavlaju (na primer broj 10 na 44. stepen). Osnovne merne jedinice za dužinu kretale su se od veličine oko pola kilometra (koja se zvala jedan li), do hiljaditih delova milimetra. Nazivi najsitnijih jedinica su: debljina vlasi kose, debljina svilene niti i zanemarljivo malo (što predstavlja trećinu mikrometra). Uprkos ovakvim nazivima, zadaci sa mernim jedinicama su primenjivani u veoma praktične svrhe, na primer, za izražavanje težine drugih vrsta zrnaste robe preko odgovarajućih mera za pirinač.
Matematika i kinesko pismo
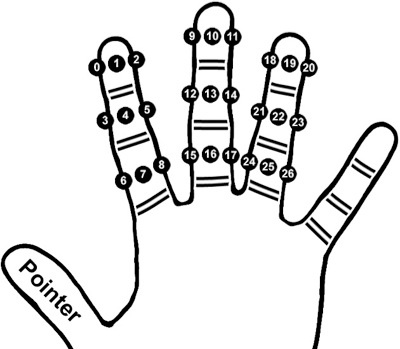
Za razliku od mnogih naroda, koji prste na šakama koriste za brojanje samo do 10, Kinezi su osmislili sistem za izvođenje računica čak do 100.000. Na svoj način su razvili i statistiku. Naime, njihova vekovna iskustva u medicini (akupunktura, akupresura, postojanje energetskih meridijana u telu…) dovela su do konkretnih rezultata zahvaljujući zaključivanju na osnovu velikog broja posmatranja, što je i danas u osnovi statističkih metoda ocenjivanja i testiranja hipoteza.
Na rane domete kineske matematike ukazuje i najpoznatija starokineska zbirka zadataka „Devet poglavlja veštine računanja”, čiji je autor nepoznat. Zbirka je nastala u vreme Han dinastije (od 206. p.n.e. do 220. n.e.) i sadrži 246 zadataka sa rešenjima, koji su podeljeni u devet celina, s obzirom na kinesko verovanje da broj 9 ima mistična svojstva. Jedan od najčuvenijih starokineskih matematičara je Liju Hui, koji je živeo u trećem veku nove ere i posebno je poznat po rešavanju zadataka u kojima treba odrediti visinu nedostupnih objekata, zbog čega ju je nazvao,,Zadaci sa morskog ostrva”. Za njega se zna da je računajući površinu pravilnog mnogougla sa 3.072 stranice koji je upisan u dati krug, dobio približnu vrednost broja „pi“ na 5 decimala (3,14159), te da se za računanje rastojanja među objektima i njihove visine služio istom metodologijom koja je nama poznata kao Pitagorina teorema.
Kinezi su se intenzivnije upoznali sa evropskom naukom tek sa dolaskom jezuitskih misionara, a prevođenje evropskih kjniga na kineski i obrnuto započeto je u 16. veku. Nastava matematike po uzoru na evropski sistem počela je u Kini tek početkom 20. veka, ali nije trebalo dugo čekati vrhunske rezultate –prvi doktorat koji je jedan Kinez odbranio na Zapadu bio je 1917. na Harvardu. Prvo učešće Kineza na međunarodnim matematičkim skupovima bilo je na Matematičkom kongresu u Cirihu 1932. godine, a Kinesko društvo matematičara je osnovano 1935. godine. Pre toga su izdavali sopstvene časopise, a interesantno je pomenuti i to da su imali svoju čuvenu porodicu matematičara – porodicu Mei, koja je živela u vreme dinastije Đing, u 17 i 18. veku. Jedan od njih je, na carski zahtev, napisao enciklopediju matematike.
Autorka studije zaključuje da Kinezima treba odati priznanje što u susretu sa evropskom naukom nisu odbacili sopstvena saznanja, pa su mnoge tradicionalne metode, uključujućii matematičke, opstale do danas. Povezanost sa matamatikom uočljiva je i u kineskom pismu: kao što će se formula 3 + 2 x 4 pisati isto svuda u svetu, a izgovarati različito, tako se i kineski slovni znakovi različito izgovaraju među etničkim grupama u Kini, ali je njihovo značenje za sve potpuno isto.
Bojana Maričić
broj 117, maj 2015.